GDPopt logic-based solver
The GDPopt solver in Pyomo allows users to solve nonlinear Generalized Disjunctive Programming (GDP) models using logic-based decomposition approaches, as opposed to the conventional approach via reformulation to a Mixed Integer Nonlinear Programming (MINLP) model.
The main advantage of these techniques is their ability to solve subproblems
in a reduced space, including nonlinear constraints only for True logical blocks.
As a result, GDPopt is most effective for nonlinear GDP models.
Three algorithms are available in GDPopt:
Logic-based outer approximation (LOA) [Turkay & Grossmann, 1996]
Global logic-based outer approximation (GLOA) [Lee & Grossmann, 2001]
Logic-based branch-and-bound (LBB) [Lee & Grossmann, 2001]
Usage and implementation details for GDPopt can be found in the PSE 2018 paper (Chen et al., 2018), or via its preprint.
Credit for prototyping and development can be found in the GDPopt class documentation, below.
GDPopt can be used to solve a Pyomo.GDP concrete model in two ways.
The simplest is to instantiate the generic GDPopt solver and specify the desired algorithm as an argument to the solve method:
>>> SolverFactory('gdpopt').solve(model, algorithm='LOA')
The alternative is to instantiate an algorithm-specific GDPopt solver:
>>> SolverFactory('gdpopt.loa').solve(model)
In the above examples, GDPopt uses the GDPopt-LOA algorithm.
Other algorithms may be used by specifying them in the algorithm argument when using the generic solver or by instantiating the algorithm-specific GDPopt solvers. All GDPopt options are listed below.
Note
The generic GDPopt solver allows minimal configuration outside of the arguments to the solve method. To avoid repeatedly specifying the same configuration options to the solve method, use the algorithm-specific solvers.
Logic-based Outer Approximation (LOA)
Chen et al., 2018 contains the following flowchart, taken from the preprint version:
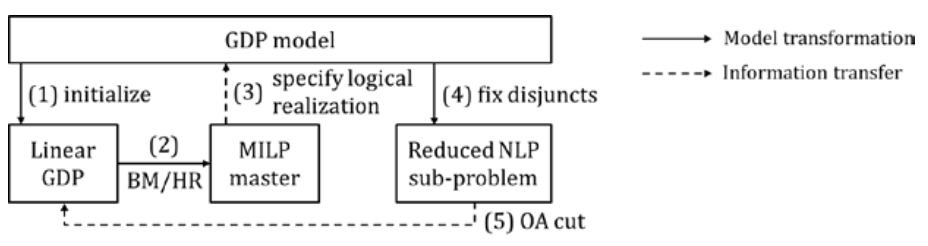
An example that includes the modeling approach may be found below.
Required imports
>>> from pyomo.environ import *
>>> from pyomo.gdp import *
Create a simple model
>>> model = ConcreteModel(name='LOA example')
>>> model.x = Var(bounds=(-1.2, 2))
>>> model.y = Var(bounds=(-10,10))
>>> model.c = Constraint(expr= model.x + model.y == 1)
>>> model.fix_x = Disjunct()
>>> model.fix_x.c = Constraint(expr=model.x == 0)
>>> model.fix_y = Disjunct()
>>> model.fix_y.c = Constraint(expr=model.y == 0)
>>> model.d = Disjunction(expr=[model.fix_x, model.fix_y])
>>> model.objective = Objective(expr=model.x + 0.1*model.y, sense=minimize)
Solve the model using GDPopt
>>> results = SolverFactory('gdpopt.loa').solve(
... model, mip_solver='glpk')
Display the final solution
>>> model.display()
Model LOA example
Variables:
x : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : -1.2 : 0.0 : 2 : False : False : Reals
y : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : -10 : 1.0 : 10 : False : False : Reals
Objectives:
objective : Size=1, Index=None, Active=True
Key : Active : Value
None : True : 0.1
Constraints:
c : Size=1
Key : Lower : Body : Upper
None : 1.0 : 1.0 : 1.0
Note
When troubleshooting, it can often be helpful to turn on verbose
output using the tee flag.
>>> SolverFactory('gdpopt.loa').solve(model, tee=True)
Global Logic-based Outer Approximation (GLOA)
The same algorithm can be used to solve GDPs involving nonconvex nonlinear constraints by solving the subproblems globally:
>>> SolverFactory('gdpopt.gloa').solve(model)
Warning
The nlp_solver option must be set to a global solver for the solution returned by GDPopt to also be globally optimal.
Relaxation with Integer Cuts (RIC)
Instead of outer approximation, GDPs can be solved using the same MILP relaxation as in the previous two algorithms, but instead of using the subproblems to generate outer-approximation cuts, the algorithm adds only no-good cuts for every discrete solution encountered:
>>> SolverFactory('gdpopt.ric').solve(model)
Again, this is a global algorithm if the subproblems are solved globally, and is not otherwise.
Note
The RIC algorithm will not necessarily enumerate all discrete solutions as it is possible for the bounds to converge first. However, full enumeration is not uncommon.
Logic-based Branch-and-Bound (LBB)
The GDPopt-LBB solver branches through relaxed subproblems with inactive disjunctions. It explores the possibilities based on best lower bound, eventually activating all disjunctions and presenting the globally optimal solution.
To use the GDPopt-LBB solver, define your Pyomo GDP model as usual:
Required imports
>>> from pyomo.environ import *
>>> from pyomo.gdp import Disjunct, Disjunction
Create a simple model
>>> m = ConcreteModel()
>>> m.x1 = Var(bounds = (0,8))
>>> m.x2 = Var(bounds = (0,8))
>>> m.obj = Objective(expr=m.x1 + m.x2, sense=minimize)
>>> m.y1 = Disjunct()
>>> m.y2 = Disjunct()
>>> m.y1.c1 = Constraint(expr=m.x1 >= 2)
>>> m.y1.c2 = Constraint(expr=m.x2 >= 2)
>>> m.y2.c1 = Constraint(expr=m.x1 >= 3)
>>> m.y2.c2 = Constraint(expr=m.x2 >= 3)
>>> m.djn = Disjunction(expr=[m.y1, m.y2])
Invoke the GDPopt-LBB solver
>>> results = SolverFactory('gdpopt.lbb').solve(m)
WARNING: 09/06/22: The GDPopt LBB algorithm currently has known issues. Please
use the results with caution and report any bugs!
>>> print(results)
>>> print(results.solver.status)
ok
>>> print(results.solver.termination_condition)
optimal
>>> print([value(m.y1.indicator_var), value(m.y2.indicator_var)])
[True, False]
GDPopt implementation and optional arguments
Warning
GDPopt optional arguments should be considered beta code and are subject to change.
- class pyomo.contrib.gdpopt.GDPopt.GDPoptSolver[source]
Decomposition solver for Generalized Disjunctive Programming (GDP) problems.
The GDPopt (Generalized Disjunctive Programming optimizer) solver applies a variety of decomposition-based approaches to solve Generalized Disjunctive Programming (GDP) problems. GDP models can include nonlinear, continuous variables and constraints, as well as logical conditions.
These approaches include:
Logic-based outer approximation (LOA)
Logic-based branch-and-bound (LBB)
Partial surrogate cuts [pending]
Generalized Bender decomposition [pending]
This solver implementation was developed by Carnegie Mellon University in the research group of Ignacio Grossmann.
For nonconvex problems, LOA may not report rigorous lower/upper bounds.
Questions: Please make a post at StackOverflow and/or contact Qi Chen <https://github.com/qtothec> or David Bernal <https://github.com/bernalde>.
Several key GDPopt components were prototyped by BS and MS students:
Logic-based branch and bound: Sunjeev Kale
MC++ interface: Johnny Bates
LOA set-covering initialization: Eloy Fernandez
Logic-to-linear transformation: Romeo Valentin
- available(exception_flag=True)[source]
Solver is always available. Though subsolvers may not be, they will raise an error when the time comes.
- solve(model, **kwds)[source]
Solve the model.
- Parameters:
model (Block) – a Pyomo model or block to be solved
- Keyword Arguments:
iterlim (NonNegativeInt, optional) – Iteration limit.
time_limit (PositiveInt, optional) – Seconds allowed until terminated. Note that the time limit can currently only be enforced between subsolver invocations. You may need to set subsolver time limits as well.
tee (bool, default=False) – Stream output to terminal.
logger (a_logger, default='pyomo.contrib.gdpopt') – The logger object or name to use for reporting.
- class pyomo.contrib.gdpopt.loa.GDP_LOA_Solver(**kwds)[source]
The GDPopt (Generalized Disjunctive Programming optimizer) logic-based outer approximation (LOA) solver.
Accepts models that can include nonlinear, continuous variables and constraints, as well as logical conditions. For nonconvex problems, LOA may not report rigorous dual bounds.
- solve(model, **kwds)[source]
Solve the model.
- Parameters:
model (Block) – the Pyomo model or block to be solved
- Keyword Arguments:
iterlim (NonNegativeInt, optional) – Iteration limit.
time_limit (PositiveInt, optional) – Seconds allowed until terminated. Note that the time limit can currently only be enforced between subsolver invocations. You may need to set subsolver time limits as well.
tee (bool, default=False) – Stream output to terminal.
logger (a_logger, default=<Logger pyomo.contrib.gdpopt (WARNING)>) – The logger object or name to use for reporting.
integer_tolerance (default=1e-05) – Tolerance on integral values.
constraint_tolerance (default=1e-06) –
Tolerance on constraint satisfaction.
Increasing this tolerance corresponds to being more conservative in declaring the model or an NLP subproblem to be infeasible.
variable_tolerance (default=1e-08) – Tolerance on variable bounds.
subproblem_initialization_method (default=<function restore_vars_to_original_values at 0x7f9b4db76d30>) –
Callback to specify custom routines for initializing the (MI)NLP subproblems. This method is called after the discrete problem solution is fixed in the subproblem and before the subproblem is solved (or pre-solved).
For algorithms with a discrete problem relaxation: This method accepts three arguments: the solver object, the subproblem GDPopt utility block and the discrete problem GDPopt utility block. The discrete problem contains the most recent discrete problem solution.
For algorithms without a discrete problem relaxation: This method accepts four arguments: the list of Disjuncts that are currently fixed as being active, a list of values for the non-indicator BooleanVars (empty if force_nlp_subproblem=False), and a list of values for the integer vars (also empty if force_nlp_subproblem=False), and last the subproblem GDPopt utility block.
The return of this method will be unused: The method should directly set the value of the variables on the subproblem
call_before_subproblem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right before the (MI)NLP subproblem is solved. Takes three arguments: The solver object, the subproblem and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
To initialize the problem before it is solved, please specify a method in the ‘subproblem_initialization_method’ argument.
call_after_subproblem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the (MI)NLP subproblem is solved. Takes three arguments: The solver object, the subproblem, and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
call_after_subproblem_feasible (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the (MI)NLP subproblem is solved, if it was feasible. Takes three arguments: The solver object, the subproblem and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
force_subproblem_nlp (default=False) – Force subproblems to be NLP, even if discrete variables exist.
subproblem_presolve (bool, default=True) – Flag to enable or disable subproblem presolve. Default=True.
tighten_nlp_var_bounds (bool, default=False) – Whether or not to do feasibility-based bounds tightening on the variables in the NLP subproblem before solving it.
round_discrete_vars (default=True) – Flag to round subproblem discrete variable values to the nearest integer. Rounding is done before fixing disjuncts.
max_fbbt_iterations (PositiveInt, default=3) – Maximum number of feasibility-based bounds tightening iterations to do during NLP subproblem preprocessing.
init_strategy (_init_strategy_deprecation, optional) – DEPRECATED: Please use ‘init_algorithm’ instead.
init_algorithm (In{'no_init': <class 'pyomo.contrib.gdpopt.util._DoNothing'>, 'set_covering': <function init_set_covering at 0x7f9b4db76b80>, 'max_binary': <function init_max_binaries at 0x7f9b4db76940>, 'fix_disjuncts': <function init_fixed_disjuncts at 0x7f9b4db76790>, 'custom_disjuncts': <function init_custom_disjuncts at 0x7f9b4db76700>}, default='set_covering') – Selects the initialization algorithm to use when generating the initial cuts to construct the discrete problem.
custom_init_disjuncts (optional) – List of disjunct sets to use for initialization.
max_slack (NonNegativeFloat, default=1000) – Upper bound on slack variables for OA
OA_penalty_factor (NonNegativeFloat, default=1000) – Penalty multiplication term for slack variables on the objective value.
set_cover_iterlim (NonNegativeInt, default=8) – Limit on the number of set covering iterations.
discrete_problem_transformation (default='gdp.bigm') – Name of the transformation to use to transform the discrete problem from a GDP to an algebraic model.
call_before_discrete_problem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right before the MILP discrete problem is solved. Takes three arguments: The solver object, the discrete problem, and the GDPopt utility block on the discrete problem.
Note that unless you are very confident in what you are doing, the problem should not be modified in this callback: it should be used to interrogate the problem only.
call_after_discrete_problem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the MILP discrete problem is solved. Takes three arguments: The solver object, the discrete problem, and the GDPopt utility block on the discrete problem.
Note that unless you are very confident in what you are doing, the problem should not be modified in this callback: it should be used to interrogate the problem only.
call_before_master_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) – DEPRECATED: Please use ‘call_before_discrete_problem_solve’
call_after_master_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) – DEPRECATED: Please use ‘call_after_discrete_problem_solve’
mip_presolve (bool, default=True) – Flag to enable or disable GDPopt MIP presolve. Default=True.
calc_disjunctive_bounds (bool, default=False) – Calculate special disjunctive variable bounds for GLOA. False by default.
obbt_disjunctive_bounds (bool, default=False) – Use optimality-based bounds tightening rather than feasibility-based bounds tightening to compute disjunctive variable bounds. False by default.
mip_solver (default='gurobi') – Mixed-integer linear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
mip_solver_args (dict, optional) – Keyword arguments to send to the MILP subsolver solve() invocation
nlp_solver (default='ipopt') – Nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
nlp_solver_args (dict, optional) – Keyword arguments to send to the NLP subsolver solve() invocation
minlp_solver (default='baron') – Mixed-integer nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
minlp_solver_args (dict, optional) – Keyword arguments to send to the MINLP subsolver solve() invocation
local_minlp_solver (default='bonmin') – Mixed-integer nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
local_minlp_solver_args (dict, optional) – Keyword arguments to send to the local MINLP subsolver solve() invocation
small_dual_tolerance (default=1e-08) – When generating cuts, small duals multiplied by expressions can cause problems. Exclude all duals smaller in absolute value than the following.
bound_tolerance (NonNegativeFloat, default=1e-06) – Tolerance for bound convergence.
- class pyomo.contrib.gdpopt.gloa.GDP_GLOA_Solver(**kwds)[source]
The GDPopt (Generalized Disjunctive Programming optimizer) global logic-based outer approximation (GLOA) solver.
Accepts models that can include nonlinear, continuous variables and constraints, as well as logical conditions.
- solve(model, **kwds)[source]
Solve the model.
- Parameters:
model (Block) – the Pyomo model or block to be solved
- Keyword Arguments:
iterlim (NonNegativeInt, optional) – Iteration limit.
time_limit (PositiveInt, optional) – Seconds allowed until terminated. Note that the time limit can currently only be enforced between subsolver invocations. You may need to set subsolver time limits as well.
tee (bool, default=False) – Stream output to terminal.
logger (a_logger, default=<Logger pyomo.contrib.gdpopt (WARNING)>) – The logger object or name to use for reporting.
integer_tolerance (default=1e-05) – Tolerance on integral values.
constraint_tolerance (default=1e-06) –
Tolerance on constraint satisfaction.
Increasing this tolerance corresponds to being more conservative in declaring the model or an NLP subproblem to be infeasible.
variable_tolerance (default=1e-08) – Tolerance on variable bounds.
subproblem_initialization_method (default=<function restore_vars_to_original_values at 0x7f9b4db76d30>) –
Callback to specify custom routines for initializing the (MI)NLP subproblems. This method is called after the discrete problem solution is fixed in the subproblem and before the subproblem is solved (or pre-solved).
For algorithms with a discrete problem relaxation: This method accepts three arguments: the solver object, the subproblem GDPopt utility block and the discrete problem GDPopt utility block. The discrete problem contains the most recent discrete problem solution.
For algorithms without a discrete problem relaxation: This method accepts four arguments: the list of Disjuncts that are currently fixed as being active, a list of values for the non-indicator BooleanVars (empty if force_nlp_subproblem=False), and a list of values for the integer vars (also empty if force_nlp_subproblem=False), and last the subproblem GDPopt utility block.
The return of this method will be unused: The method should directly set the value of the variables on the subproblem
call_before_subproblem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right before the (MI)NLP subproblem is solved. Takes three arguments: The solver object, the subproblem and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
To initialize the problem before it is solved, please specify a method in the ‘subproblem_initialization_method’ argument.
call_after_subproblem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the (MI)NLP subproblem is solved. Takes three arguments: The solver object, the subproblem, and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
call_after_subproblem_feasible (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the (MI)NLP subproblem is solved, if it was feasible. Takes three arguments: The solver object, the subproblem and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
force_subproblem_nlp (default=False) – Force subproblems to be NLP, even if discrete variables exist.
subproblem_presolve (bool, default=True) – Flag to enable or disable subproblem presolve. Default=True.
tighten_nlp_var_bounds (bool, default=False) – Whether or not to do feasibility-based bounds tightening on the variables in the NLP subproblem before solving it.
round_discrete_vars (default=True) – Flag to round subproblem discrete variable values to the nearest integer. Rounding is done before fixing disjuncts.
max_fbbt_iterations (PositiveInt, default=3) – Maximum number of feasibility-based bounds tightening iterations to do during NLP subproblem preprocessing.
init_strategy (_init_strategy_deprecation, optional) – DEPRECATED: Please use ‘init_algorithm’ instead.
init_algorithm (In{'no_init': <class 'pyomo.contrib.gdpopt.util._DoNothing'>, 'set_covering': <function init_set_covering at 0x7f9b4db76b80>, 'max_binary': <function init_max_binaries at 0x7f9b4db76940>, 'fix_disjuncts': <function init_fixed_disjuncts at 0x7f9b4db76790>, 'custom_disjuncts': <function init_custom_disjuncts at 0x7f9b4db76700>}, default='set_covering') – Selects the initialization algorithm to use when generating the initial cuts to construct the discrete problem.
custom_init_disjuncts (optional) – List of disjunct sets to use for initialization.
max_slack (NonNegativeFloat, default=1000) – Upper bound on slack variables for OA
OA_penalty_factor (NonNegativeFloat, default=1000) – Penalty multiplication term for slack variables on the objective value.
set_cover_iterlim (NonNegativeInt, default=8) – Limit on the number of set covering iterations.
discrete_problem_transformation (default='gdp.bigm') – Name of the transformation to use to transform the discrete problem from a GDP to an algebraic model.
call_before_discrete_problem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right before the MILP discrete problem is solved. Takes three arguments: The solver object, the discrete problem, and the GDPopt utility block on the discrete problem.
Note that unless you are very confident in what you are doing, the problem should not be modified in this callback: it should be used to interrogate the problem only.
call_after_discrete_problem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the MILP discrete problem is solved. Takes three arguments: The solver object, the discrete problem, and the GDPopt utility block on the discrete problem.
Note that unless you are very confident in what you are doing, the problem should not be modified in this callback: it should be used to interrogate the problem only.
call_before_master_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) – DEPRECATED: Please use ‘call_before_discrete_problem_solve’
call_after_master_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) – DEPRECATED: Please use ‘call_after_discrete_problem_solve’
mip_presolve (bool, default=True) – Flag to enable or disable GDPopt MIP presolve. Default=True.
calc_disjunctive_bounds (bool, default=False) – Calculate special disjunctive variable bounds for GLOA. False by default.
obbt_disjunctive_bounds (bool, default=False) – Use optimality-based bounds tightening rather than feasibility-based bounds tightening to compute disjunctive variable bounds. False by default.
mip_solver (default='gurobi') – Mixed-integer linear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
mip_solver_args (dict, optional) – Keyword arguments to send to the MILP subsolver solve() invocation
nlp_solver (default='couenne') – Nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
nlp_solver_args (dict, optional) – Keyword arguments to send to the NLP subsolver solve() invocation
minlp_solver (default='baron') – Mixed-integer nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
minlp_solver_args (dict, optional) – Keyword arguments to send to the MINLP subsolver solve() invocation
local_minlp_solver (default='bonmin') – Mixed-integer nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
local_minlp_solver_args (dict, optional) – Keyword arguments to send to the local MINLP subsolver solve() invocation
small_dual_tolerance (default=1e-08) – When generating cuts, small duals multiplied by expressions can cause problems. Exclude all duals smaller in absolute value than the following.
bound_tolerance (NonNegativeFloat, default=1e-06) – Tolerance for bound convergence.
- class pyomo.contrib.gdpopt.ric.GDP_RIC_Solver(**kwds)[source]
The GDPopt (Generalized Disjunctive Programming optimizer) relaxation with integer cuts (RIC) solver.
Accepts models that can include nonlinear, continuous variables and constraints, as well as logical conditions. For non-convex problems, RIC will not be exact unless the NLP subproblems are solved globally.
- solve(model, **kwds)[source]
Solve the model.
- Parameters:
model (Block) – the Pyomo model or block to be solved
- Keyword Arguments:
iterlim (NonNegativeInt, optional) – Iteration limit.
time_limit (PositiveInt, optional) – Seconds allowed until terminated. Note that the time limit can currently only be enforced between subsolver invocations. You may need to set subsolver time limits as well.
tee (bool, default=False) – Stream output to terminal.
logger (a_logger, default=<Logger pyomo.contrib.gdpopt (WARNING)>) – The logger object or name to use for reporting.
mip_solver (default='gurobi') – Mixed-integer linear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
mip_solver_args (dict, optional) – Keyword arguments to send to the MILP subsolver solve() invocation
nlp_solver (default='ipopt') – Nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
nlp_solver_args (dict, optional) – Keyword arguments to send to the NLP subsolver solve() invocation
minlp_solver (default='baron') – Mixed-integer nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
minlp_solver_args (dict, optional) – Keyword arguments to send to the MINLP subsolver solve() invocation
local_minlp_solver (default='bonmin') – Mixed-integer nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
local_minlp_solver_args (dict, optional) – Keyword arguments to send to the local MINLP subsolver solve() invocation
small_dual_tolerance (default=1e-08) – When generating cuts, small duals multiplied by expressions can cause problems. Exclude all duals smaller in absolute value than the following.
bound_tolerance (NonNegativeFloat, default=1e-06) – Tolerance for bound convergence.
integer_tolerance (default=1e-05) – Tolerance on integral values.
constraint_tolerance (default=1e-06) –
Tolerance on constraint satisfaction.
Increasing this tolerance corresponds to being more conservative in declaring the model or an NLP subproblem to be infeasible.
variable_tolerance (default=1e-08) – Tolerance on variable bounds.
subproblem_initialization_method (default=<function restore_vars_to_original_values at 0x7f9b4db76d30>) –
Callback to specify custom routines for initializing the (MI)NLP subproblems. This method is called after the discrete problem solution is fixed in the subproblem and before the subproblem is solved (or pre-solved).
For algorithms with a discrete problem relaxation: This method accepts three arguments: the solver object, the subproblem GDPopt utility block and the discrete problem GDPopt utility block. The discrete problem contains the most recent discrete problem solution.
For algorithms without a discrete problem relaxation: This method accepts four arguments: the list of Disjuncts that are currently fixed as being active, a list of values for the non-indicator BooleanVars (empty if force_nlp_subproblem=False), and a list of values for the integer vars (also empty if force_nlp_subproblem=False), and last the subproblem GDPopt utility block.
The return of this method will be unused: The method should directly set the value of the variables on the subproblem
call_before_subproblem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right before the (MI)NLP subproblem is solved. Takes three arguments: The solver object, the subproblem and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
To initialize the problem before it is solved, please specify a method in the ‘subproblem_initialization_method’ argument.
call_after_subproblem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the (MI)NLP subproblem is solved. Takes three arguments: The solver object, the subproblem, and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
call_after_subproblem_feasible (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the (MI)NLP subproblem is solved, if it was feasible. Takes three arguments: The solver object, the subproblem and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
force_subproblem_nlp (default=False) – Force subproblems to be NLP, even if discrete variables exist.
subproblem_presolve (bool, default=True) – Flag to enable or disable subproblem presolve. Default=True.
tighten_nlp_var_bounds (bool, default=False) – Whether or not to do feasibility-based bounds tightening on the variables in the NLP subproblem before solving it.
round_discrete_vars (default=True) – Flag to round subproblem discrete variable values to the nearest integer. Rounding is done before fixing disjuncts.
max_fbbt_iterations (PositiveInt, default=3) – Maximum number of feasibility-based bounds tightening iterations to do during NLP subproblem preprocessing.
init_strategy (_init_strategy_deprecation, optional) – DEPRECATED: Please use ‘init_algorithm’ instead.
init_algorithm (In{'no_init': <class 'pyomo.contrib.gdpopt.util._DoNothing'>, 'set_covering': <function init_set_covering at 0x7f9b4db76b80>, 'max_binary': <function init_max_binaries at 0x7f9b4db76940>, 'fix_disjuncts': <function init_fixed_disjuncts at 0x7f9b4db76790>, 'custom_disjuncts': <function init_custom_disjuncts at 0x7f9b4db76700>}, default='set_covering') – Selects the initialization algorithm to use when generating the initial cuts to construct the discrete problem.
custom_init_disjuncts (optional) – List of disjunct sets to use for initialization.
max_slack (NonNegativeFloat, default=1000) – Upper bound on slack variables for OA
OA_penalty_factor (NonNegativeFloat, default=1000) – Penalty multiplication term for slack variables on the objective value.
set_cover_iterlim (NonNegativeInt, default=8) – Limit on the number of set covering iterations.
discrete_problem_transformation (default='gdp.bigm') – Name of the transformation to use to transform the discrete problem from a GDP to an algebraic model.
call_before_discrete_problem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right before the MILP discrete problem is solved. Takes three arguments: The solver object, the discrete problem, and the GDPopt utility block on the discrete problem.
Note that unless you are very confident in what you are doing, the problem should not be modified in this callback: it should be used to interrogate the problem only.
call_after_discrete_problem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the MILP discrete problem is solved. Takes three arguments: The solver object, the discrete problem, and the GDPopt utility block on the discrete problem.
Note that unless you are very confident in what you are doing, the problem should not be modified in this callback: it should be used to interrogate the problem only.
call_before_master_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) – DEPRECATED: Please use ‘call_before_discrete_problem_solve’
call_after_master_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) – DEPRECATED: Please use ‘call_after_discrete_problem_solve’
mip_presolve (bool, default=True) – Flag to enable or disable GDPopt MIP presolve. Default=True.
calc_disjunctive_bounds (bool, default=False) – Calculate special disjunctive variable bounds for GLOA. False by default.
obbt_disjunctive_bounds (bool, default=False) – Use optimality-based bounds tightening rather than feasibility-based bounds tightening to compute disjunctive variable bounds. False by default.
- class pyomo.contrib.gdpopt.branch_and_bound.GDP_LBB_Solver(**kwds)[source]
The GDPopt (Generalized Disjunctive Programming optimizer) logic-based branch and bound (LBB) solver.
Accepts models that can include nonlinear, continuous variables and constraints, as well as logical conditions.
- solve(model, **kwds)[source]
Solve the model.
- Parameters:
model (Block) – the Pyomo model or block to be solved
- Keyword Arguments:
iterlim (NonNegativeInt, optional) – Iteration limit.
time_limit (PositiveInt, optional) – Seconds allowed until terminated. Note that the time limit can currently only be enforced between subsolver invocations. You may need to set subsolver time limits as well.
tee (bool, default=False) – Stream output to terminal.
logger (a_logger, default=<Logger pyomo.contrib.gdpopt (WARNING)>) – The logger object or name to use for reporting.
mip_solver (default='gurobi') – Mixed-integer linear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
mip_solver_args (dict, optional) – Keyword arguments to send to the MILP subsolver solve() invocation
nlp_solver (default='ipopt') – Nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
nlp_solver_args (dict, optional) – Keyword arguments to send to the NLP subsolver solve() invocation
minlp_solver (default='baron') – Mixed-integer nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
minlp_solver_args (dict, optional) – Keyword arguments to send to the MINLP subsolver solve() invocation
local_minlp_solver (default='bonmin') – Mixed-integer nonlinear solver to use. Note that no persisent solvers other than the auto-persistent solvers in the APPSI package are supported.
local_minlp_solver_args (dict, optional) – Keyword arguments to send to the local MINLP subsolver solve() invocation
small_dual_tolerance (default=1e-08) – When generating cuts, small duals multiplied by expressions can cause problems. Exclude all duals smaller in absolute value than the following.
integer_tolerance (default=1e-05) – Tolerance on integral values.
constraint_tolerance (default=1e-06) –
Tolerance on constraint satisfaction.
Increasing this tolerance corresponds to being more conservative in declaring the model or an NLP subproblem to be infeasible.
variable_tolerance (default=1e-08) – Tolerance on variable bounds.
subproblem_initialization_method (default=<function restore_vars_to_original_values at 0x7f9b4db76d30>) –
Callback to specify custom routines for initializing the (MI)NLP subproblems. This method is called after the discrete problem solution is fixed in the subproblem and before the subproblem is solved (or pre-solved).
For algorithms with a discrete problem relaxation: This method accepts three arguments: the solver object, the subproblem GDPopt utility block and the discrete problem GDPopt utility block. The discrete problem contains the most recent discrete problem solution.
For algorithms without a discrete problem relaxation: This method accepts four arguments: the list of Disjuncts that are currently fixed as being active, a list of values for the non-indicator BooleanVars (empty if force_nlp_subproblem=False), and a list of values for the integer vars (also empty if force_nlp_subproblem=False), and last the subproblem GDPopt utility block.
The return of this method will be unused: The method should directly set the value of the variables on the subproblem
call_before_subproblem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right before the (MI)NLP subproblem is solved. Takes three arguments: The solver object, the subproblem and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
To initialize the problem before it is solved, please specify a method in the ‘subproblem_initialization_method’ argument.
call_after_subproblem_solve (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the (MI)NLP subproblem is solved. Takes three arguments: The solver object, the subproblem, and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
call_after_subproblem_feasible (default=<class 'pyomo.contrib.gdpopt.util._DoNothing'>) –
Callback called right after the (MI)NLP subproblem is solved, if it was feasible. Takes three arguments: The solver object, the subproblem and the GDPopt utility block on the subproblem.
Note that unless you are very confident in what you are doing, the subproblem should not be modified in this callback: it should be used to interrogate the problem only.
force_subproblem_nlp (default=False) – Force subproblems to be NLP, even if discrete variables exist.
subproblem_presolve (bool, default=True) – Flag to enable or disable subproblem presolve. Default=True.
tighten_nlp_var_bounds (bool, default=False) – Whether or not to do feasibility-based bounds tightening on the variables in the NLP subproblem before solving it.
round_discrete_vars (default=True) – Flag to round subproblem discrete variable values to the nearest integer. Rounding is done before fixing disjuncts.
max_fbbt_iterations (PositiveInt, default=3) – Maximum number of feasibility-based bounds tightening iterations to do during NLP subproblem preprocessing.
bound_tolerance (NonNegativeFloat, default=1e-06) – Tolerance for bound convergence.
check_sat (bool, default=False) – When True, GDPopt-LBB will check satisfiability at each node via the pyomo.contrib.satsolver interface
solve_local_rnGDP (bool, default=False) – When True, GDPopt-LBB will solve a local MINLP at each node.